In this Session XII : Functional Programming Language, there are 7 subtopics:

• Introduction
• Mathematical Functions
• Fundamentals of Functional Programming Languages
• The First Functional Programming Language: LISP
• Introduction to Scheme
• Common LISP
• Comparison of Functional and Imperative Languages

Introduction

The design of the imperative languages is based directly on the von Neumann architecture  as discussed in Chapter 1. Imperative languages can be thought of collectively as a progression of developments to improve the basic model, which was Fortran I. All have been designed to make efficient use of von Neumann architecture computers. Although the imperative style of programming has been found acceptable by most programmers, its heavy reliance on the underlying architecture is thought by some to be an unnecessary restriction on the alternative approaches to software development. Other bases for language design exist, some of them oriented more to particular programming paradigms or methodologies than to efficient execution on a particular computer architecture. Thus far, however, only a relatively small minority of programs have been written in nonimperative languages. The functional programming paradigm, which is based on mathematical functions, is the design basis of the most important nonimperative styles of languages. This style of programming is supported by functional programming languages.

Mathematical Functions

A mathematical function is a mapping of members of one set, called the domain set, to another set, called the range set. A function definition specifies the domain and range sets, either explicitly or implicitly, along with the mapping. The mapping is described by an expression or, in some cases, by a table. Functions are often applied to a particular element of the domain set, given as a parameter to the function.

Lambda Expression

A lambda expression specifies the parameters and the mapping of a function. The lambda expression is the function itself, which is nameless

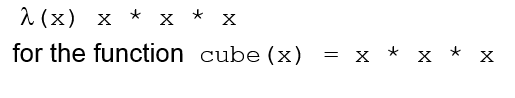
Lambda expressions describe nameless functions and are applied to parameter(s) by placing the parameter(s) after the expression

Functional Forms

A higher-order function, or functional form, is one that either takes one or more functions as parameters or yields a function as its result, or both. One common kind of functional form is function composition, which has two functional parameters and yields a function whose value is the first actual parameter function applied to the result of the second.

Function Composition

Function Composition is a functional form that takes two functions as parameters and yields a function whose value is the first actual parameter function applied to the application of the second.

Apply-to-all

Apply-to-all is a functional form that takes a single function as a parameter and yields a list of values obtained by applying the given function to each element of a list of parameters

Fundamentals of Functional Programming Languages

The objective of the design of a functional programming language is to mimic mathematical functions to the greatest extent possible. This results in an approach to problem solving that is fundamentally different from approaches used with imperative languages. In an imperative language, an expression is evaluated and the result is stored in a memory location, which is represented as a variable in a program. This is the purpose of assignment statements. This necessary attention to memory cells, whose values represent the state of the program, results in a relatively low-level programming methodology.

A purely functional programming language does not use variables or assignment statements, thus freeing the programmer from concerns related to the memory cells, or state, of the program. Without variables, iterative constructs are not possible, for they are controlled by variables. Repetition must be specified with recursion rather than with iteration. Programs are function definitions and function application specifications, and executions consist of evaluating function applications. Without variables, the execution of a purely functional program has no state in the sense of operational and denotational semantics. The execution of a function always produces the same result when given the same parameters. This feature is called referential transparency. It makes the semantics of purely functional languages far simpler than the semantics of the imperative languages (and the functional languages that include imperative features). It also makes testing easier, because each function can be tested separately, without any concern for its context.

The first functional programming language, LISP, uses a syntactic form, for both data and code, that is very different from that of the imperative languages. However, many functional languages designed later use syntax for their code that is similar to that of the imperative languages

The First Functional Programming Language: LISP

There were only two categories of data objects in the original LISP: atoms and lists. List elements are pairs, where the first part is the data of the element, which is a pointer to either an atom or a nested list. The second part of a pair can be a pointer to an atom, a pointer to another element, or the empty list. Elements are linked together in lists with the second parts. Atoms and lists are not types in the sense that imperative languages have types. In fact, the original LISP was a typeless language. Atoms are either symbols, in the form of identifiers, or numeric literals. Lambda notation is used to specify functions and function definitions. Function applications and data have the same form. The first LISP interpreter appeared only as a  demonstration of the universality of the computational capabilities of the notation

Introduction to Scheme

The Scheme language, which is a dialect of LISP, was developed at MIT. It is characterized by its small size, its exclusive use of static scoping, and its treatment of functions as first-class entities. As first-class entities, Scheme functions can be the values of expressions, elements of lists, passed as parameters, and returned from functions.

A Scheme interpreter in interactive mode is an infinite read-evaluate-print loop (often abbreviated as REPL). It repeatedly reads an expression typed by the user (in the form of a list), interprets the expression, and displays the resulting value. This form of interpreter is also used by Ruby and Python. Expressions are interpreted by the function EVAL. Literals evaluate to themselves. So, if you type a number to the interpreter, it simply displays the number. A Scheme program is a collection of function definitions. Consequently, knowing how to define these functions is a prerequisite to writing the simplest program. In Scheme, a nameless function actually includes the word LAMBDA, and is called a lambda expression.

Scheme includes a few simple output functions, but when used with the interactive interpreter, most output from Scheme programs is the normal output from the interpreter, displaying the results of applying EVAL to top-level functions. Scheme includes a formatted output function, PRINTF, which is similar to the printf function of C.

A predicate function is one that returns a Boolean value (some representation of either true or false). Scheme includes a collection of predicate functions for numeric data. When a list is interpreted as a Boolean, any nonempty list evaluates to true; the empty list evaluates to false. This is similar to the interpretation of integers in C as Boolean values; zero evaluates to false and any nonzero value evaluates to true. Scheme uses three different constructs for control flow: one similar to the selection construct of the imperative languages and two based on the evaluation control used in mathematical functions.

Scheme programs are interpreted by the function application function, EVAL. When applied to a primitive function, EVAL first evaluates the parameters of the given function. This action is necessary when the actual parameters in a function call are themselves function calls, which is frequently the case. In some calls, however, the parameters are data elements rather than function references. When a parameter is not a function reference, it obviously should not be evaluated.

Common LISP

Common LISP was created in an effort to combine the features of several early 1980s dialects of LISP, including Scheme, into a single language. Being something of a union of languages, it is quite large and complex, similar in these regards to C++ and C#. Its basis, however, is the original LISP, so its syntax, primitive functions, and fundamental nature come from that language.

The list of features of Common LISP is long: a large number of data types and structures, including records, arrays, complex numbers, and character strings; powerful input and output operations; and a form of packages for modularizing collections of functions and data, and also for providing access control. Common LISP includes several imperative constructs, as well as some mutable types. Recognizing the occasional flexibility provided by dynamic scoping, as well as the simplicity of static scoping, Common LISP allows both. The default scoping for variables is static, but by declaring a variable to be “special,” that variable becomes dynamically scoped. Macros are often used in Common LISP to extend the language. In fact, some of the predefined functions are actually macros. For example, DOLIST, which takes two parameters, a variable and a list, is a macro.

LISP implementations have a front end called the reader that transforms the text of LISP programs into a code representation. Then, the macro calls in the code representation are expanded into code representations. The output of this step is then either interpreted or compiled into the machine language of the host computer, or perhaps into an intermediate code than can be interpreted. There is a special kind of macro, named reader macros or read macros, that are expanded during the reader phase of a LISP language processor. A reader macro expands a specific character into a string of LISP code. For example, the apostrophe in LISP is a read macro that expands to a call to QUOTE. Users can define their own reader macros to create other shorthand constructs.

Comparison of Functional and Imperative Languages

Some in the functional programming community have claimed that the use of functional programming results in an order-of-magnitude increase in productivity, largely due to functional programs being claimed to be only 10 percent as large as their imperative counterparts. While such numbers have been actually shown for certain problem areas, for other problem areas, functional programs are more like 25 percent as large as imperative solutions to the same problems. These factors allow proponents of functional programming to claim productivity advantages over imperative programming of 4 to 10 times. However, program size alone is not necessarily a good measure of productivity. Certainly not all lines of source code have equal complexity, nor do they take the same amount of time to produce. In fact, because of the necessity of dealing with variables, imperative programs have many trivially simple lines for initializing and making small changes to variables. Execution efficiency is another basis for comparison. When functional programs are interpreted, they are of course much slower than their compiled imperative counterparts. However, there are now compilers for most functional languages, so that execution speed disparities between functional languages and compiled imperative languages are no longer so great. One might be tempted to say that because functional programs are significantly smaller than equivalent imperative programs, they should execute much faster than the imperative programs. However, this often is not the case, because of a collection of language characteristics of the functional languages, such as lazy evaluation, that have a negative impact on execution efficiency. Considering the relative efficiency of functional and imperative programs, it is reasonable to estimate that an average functional program will execute in about twice the time of its imperative counterpart.

One simple factor that strongly affects the complexity of imperative, or procedural programming, is the necessary attention of the programmer to the state of the program at each step of its development. In a large program, the state of the program is a large number of values (for the large number of program variables). In pure functional programming, there is no state; hence, no need to devote attention to keeping it in mind. It is not a simple matter to determine precisely why functional languages have not attained greater popularity. The inefficiency of the early implementations was clearly a factor then, and it is likely that at least some contemporary imperative programmers still believe that programs written in functional languages are slow. In addition, the vast majority of programmers learn programming using imperative languages, which makes functional programs appear to them to be strange and difficult to understand.