In this Session XIII : Logic Programming Language, there are 7 subtopics:

• Introduction
• A Brief Introduction to Predicate Calculus
• An Overview of Logic Programming
• The Origins of Prolog
• The Basic Elements of Prolog
• Deficiencies of Prolog
• Applications of Logic Programming

Introduction

Programming that uses a form of symbolic logic as a programming language is often called logic programming, and languages based on symbolic logic are called logic programming languages, or declarative languages. We have chosen to describe the logic programming language Prolog, because it is the only widely used logic language. The syntax of logic programming languages is remarkably different from that of the imperative and functional languages. The semantics of logic programs also bears little resemblance to that of imperative-language programs. These observations should lead the reader to some curiosity about the nature of logic programming and declarative languages.

 

A Brief Introduction to Predicate Calculus

A proposition can be thought of as a logical statement that may or may not be true. It consists of objects and the relationships among objects. Formal logic was developed to provide a method for describing propositions, with the goal of allowing those formally stated propositions to be checked for validity.

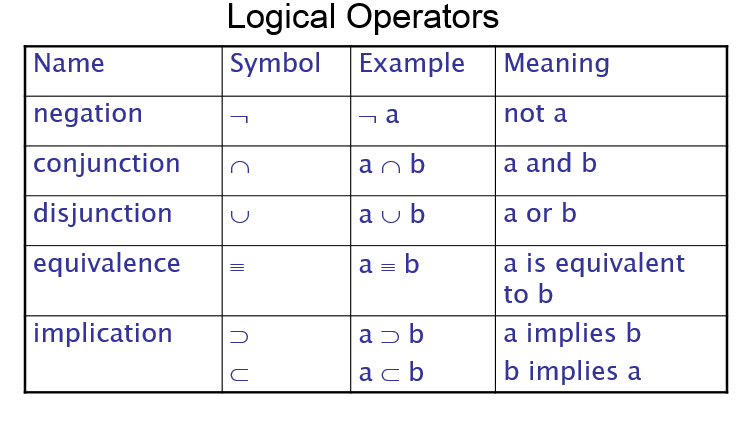
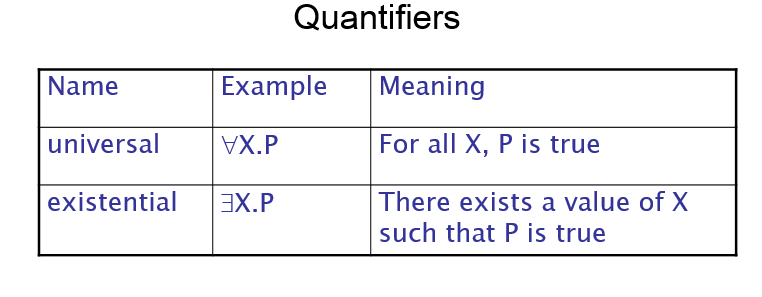
Symbolic logic can be used for the three basic needs of formal logic: to express propositions, to express the relationships between propositions, and to describe how new propositions can be inferred from other propositions that are assumed to be true. Particular form of symbolic logic used for logic programming called predicate calculus

Propositions

The objects in logic programming propositions are represented by simple terms, which are either constants or variables. A constant is a symbol that represents an object. A variable is a symbol that can represent different objects at different times, although in a sense that is far closer to mathematics than the variables in an imperative programming language. The simplest propositions, which are called atomic propositions, consist of compound terms. A compound term is one element of a mathematical relation, written in a form that has the appearance of mathematical function notation.

Clausal Form

One problem with predicate calculus as we have described it thus far is that there are too many different ways of stating propositions that have the same meaning; that is, there is a great deal of redundancy. This is not such a problem for logicians, but if predicate calculus is to be used in an automated (computerized) system, it is a serious problem. To simplify matters, a standard form for propositions is desirable. Clausal form, which is a relatively simple form of propositions, is one such standard form. All propositions can be expressed in clausal form.

An Overview of Logic Programming

Languages used for logic programming are called declarative languages, because programs written in them consist of declarations rather than assignments and control flow statements. These declarations are actually statements, or propositions, in symbolic logic. One of the essential characteristics of logic programming languages is their semantics, which is called declarative semantics. The basic concept of this semantics is that there is a simple way to determine the meaning of each statement, and it does not depend on how the statement might be used to solve a problem. Declarative semantics is considerably simpler than the semantics of the imperative languages.

Programming in a logic programming language is nonprocedural. Programs in such languages do not state exactly how a result is to be computed but rather describe the form of the result. The difference is that we assume the computer system can somehow determine how the result is to be computed. What is needed to provide this capability for logic programming languages is a concise means of supplying the computer with both the relevant information and a method of inference for computing desired results.

The Origins of Prolog

Alain Colmerauer and Phillippe Roussel at the University of Aix-Marseille, with some assistance from Robert Kowalski at the University of Edinburgh, developed the fundamental design of Prolog. The collaboration between the University of Aix-Marseille and the University of Edinburgh continued until the mid-1970s. Since then, research on the development and use of the language has progressed independently at those two locations, resulting in, among other things, two syntactically different dialects of Prolog.

After a decade of effort, the FGCS project was quietly dropped. Despite the great assumed potential of logic programming and Prolog, little of great significance had been discovered. This led to the decline in the interest in and use of Prolog, although it still has its applications and proponents.

The Basic Elements of Prolog

There are now a number of different dialects of Prolog. These can be grouped into several categories: those that grew from the Marseille group, those that came from the Edinburgh group, and some dialects that have been developed for microcomputers, such as micro-Prolog, which is described by Clark and McCabe.

Terms

A Prolog term is a constant, a variable, or a structure. A constant is either an atom or an integer. Atoms are the symbolic values of Prolog and are similar to their counterparts in LISP. In particular, an atom is either a string of letters, digits, and underscores that begins with a lowercase letter or a string of any printable ASCII characters delimited by apostrophes.

A variable is any string of letters, digits, and underscores that begins with an uppercase letter or an underscore ( _ ). Variables are not bound to types by declarations. The binding of a value, and thus a type, to a variable is called an instantiation. Instantiation occurs only in the resolution process. A variable that has not been assigned a value is called uninstantiated. Instantiations last only as long as it takes to satisfy one complete goal, which involves the proof or disproof of one proposition. Prolog variables are only distant relatives, in terms of both semantics and use, to the variables in the imperative languages. The last kind of term is called a structure. Structures represent the atomic propositions of predicate calculus, and their general form is the same.

Fact Statements

Our discussion of Prolog statements begins with those statements used to construct the hypotheses, or database of assumed information—the statements from which new information can be inferred.

Rule Statements

Rule Statements are also used for hypotheses. The other basic form of Prolog statement for constructing the database corresponds to a headed Horn clause. This form can be related to a known theorem in mathematics from which a conclusion can be drawn if the set of given conditions is satisfied.

The right side is the antecedent, or if part, and the left side is the consequent, or then part. If the antecedent of a Prolog statement is true, then the consequent of the statement must also be true. Because they are Horn clauses, the consequent of a Prolog statement is a single term, while the antecedent can be either a single term or a conjunction.

Goal Statements

In Prolog, these propositions are called goals, or queries. The syntactic form of Prolog goal statements is identical to that of headless Horn clauses. Goal Statements are used for theorem proving, theorem is in form of proposition that we want system to prove or disprove – goal statement. 

The Inferencing Process of Prolog

Queries are called goals. When a goal is a compound proposition, each of the facts (structures) is called a subgoal. To prove that a goal is true, the inferencing process must find a chain of inference rules and/or facts in the database that connect the goal to one or more facts in the database.

When goal has more than one subgoal, can use either

• Depth-first search: find a complete proof for the first subgoal before working on others
• Breadth-first search: work on all subgoals in parallel

Backtracking is a condition with a goal with multiple subgoals, if fail to show truth of one of subgoals, reconsider previous subgoal to find an alternative solution.

There are two opposite approaches to attempting to match a given goal to a fact in the database. The system can begin with the facts and rules of the database and attempt to find a sequence of matches that lead to the goal. This approach is called bottom-up resolution, or forward chaining. The alternative is to begin with the goal and attempt to find a sequence of matching propositions that lead to some set of original facts in the database. This approach is called top-down resolution, or backward chaining.

Simple Arithmetic

Prolog supports integer variables and integer arithmetic.  is operator: takes an arithmetic expression as right operand and variable as left operand. Example :

It is instructive to take an operational look at how a Prolog system produces results. Prolog has a built-in structure named trace that displays the instantiations of values to variables at each step during the attempt to satisfy a given goal. trace is used to understand and debug Prolog programs.

List Structures

List is a sequence of any number of elements. Elements can be atoms, atomic propositions, or other terms (including other lists)

Append example :

Deficiencies of Prolog

Prolog, for reasons of efficiency, allows the user to control the ordering of pattern matching during resolution. In a pure logic programming environment, the order of attempted matches that take place during resolution is nondeterministic, and all matches could be attempted concurrently. However, because Prolog always matches in the same order, starting at the beginning of the database and at the left end of a given goal, the user can profoundly affect efficiency by ordering the database statements to optimize a particular application. For example, if the user knows that certain rules are much more likely to succeed than the others during a particular “execution,” then the program can be made more efficient by placing those rules first in the database.

Applications of Logic Programming

Relational database management systems

Relational database management systems (RDBMSs) store data in the form of tables. Queries on such databases are often stated in Structured Query Language (SQL). SQL is nonprocedural in the same sense that logic programming is nonprocedural. The user does not describe how to retrieve the answer; rather, he or she describes only the characteristics of the answer. The connection between logic programming and RDBMSs should be obvious. Simple tables of information can be described by Prolog structures, and relationships between tables can be conveniently and easily described by Prolog rules. The retrieval process is inherent in the resolution operation. The goal statements of Prolog provide the queries for the RDBMS. Logic programming is thus a natural match to the needs of implementing an RDBMS.

Expert systems

Expert systems are computer systems designed to emulate human expertise in some particular domain. They consist of a database of facts, an inferencing process, some heuristics about the domain, and some friendly human interface that makes the system appear much like an expert human consultant. In addition to their initial knowledge base, which is provided by a human expert, expert systems learn from the process of being used, so their databases must be capable of growing dynamically. Also, an expert system should include the capability of interrogating the user to get additional information when it determines that such information is needed.

Natural language processing

Certain kinds of natural-language processing can be done with logic programming. In particular, natural-language interfaces to computer software systems, such as intelligent databases and other intelligent knowledge-based systems, can be conveniently done with logic programming. For describing language syntax, forms of logic programming have been found to be equivalent to context-free grammars. Proof procedures in logic programming systems have been found to be equivalent to certain parsing strategies.